数据结构之链表

本篇文章可以收获的知识：

什么是链表
链表的常用操作与数组的对比
四道LeetCode算法题巩固链表
如何分析时间复杂度和空间复杂度
详解JavaScript中的原型链
详解instanceof的原理
使用链表指针获取JSON 的节点值

什么是链表

链表是由多个元素组成的列表，元素存储是不连续的，元素之间用next指针连在一起，在JavaScript中没有链表，使用Object来模拟链表的功能。

链表的常用操作

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */

const n1 = new ListNode(1) // 链表1
const n2 = new ListNode(2) // 链表2
const n3 = new ListNode(3) // 链表3
n1.next = n2 // 给n1链表，插入元素
n2.next = n3 // 给n2链表，插入元素
n1.next = n3 // 删除n2元素，一开始n1的指针指向n2的，让n1的指针指向n3就删除n2

// 遍历链表操作
// 思路
// 定义一个指针
// 循环遍历指针，访问当前指针，指针指向下一针，直到指针为空
let p = n1;
while(p) {
  console.log(p.val)
  p = p.next;
}

了解了链表的操作之后，我们会发现链表的新增元素和删除元素只需要修改某个指针就能实现需求，而数组在这些操作之后，需要移动元素来实现（除操作首尾元素），所以做增删操作的时候，链表的性能是比数据的性能高的。

LeetCode算法题：题号237，删除链表中的节点

其实这道题相对简单，做题人一开始的思路肯定是让传进来的node的上一个元素的next指向node的下一个元素就可以了，但是我们并不知道node的上一个元素，所以我们可以在node的下一个元素做文章。

解题思路：

不能拿到node的上一个元素，只能拿到node的下一个元素
将node的元素替换成node的下一个元素

解题步骤：

将node的下一个元素的值赋值给node
让node的下一个元素指向node的下下个元素

代码实现：

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} node
 * @return {void} Do not return anything, modify node in-place instead.
 */
var deleteNode = function(node) {
  node.val = node.next.val;
  node.next = node.next.next;
};

这道题因为没有循环体，没有额外的产生数据结构，所以时间复杂度和空间复杂度都是O(1)。

LeetCode算法题：题号206，反转链表

方法一，正向反转指针：

解题思路：

反转两个节点，将n+1的指针指向n
反转多个节点，重复上面的操作就能实现。

解题步骤：

一定一前一后指针，遍历链表
反转指针

代码实现：

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function(head) {
  let p1 = null;
  let p2 = head
  while(p2) {
    const tmp = p2.next;
    p2.next = p1;
    p1 = p2;
    p2 = tmp
  }
  return p1;
};

因为代码中有个while循环体，循环的次数是传进来的链表长度，所以时间复杂度是O(n)，n是链表的长度。

因为代码中没有产生额外的数据结构，所以空间复杂度是O(1)。

方法二，反向反转指针：

解题思路：

反向反转指针，从链表的尾指针开始反转指针
这个场景非常适合递归来实现

解题步骤：

两个节点的反转，让当前指针的下下指针等于当前指针，然后将当前的下个指针等于null，解决闭环问题。
重复上一步骤

代码实现：

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function(head) {
  if (head === null || head.next === null) {
    return head;
  }
  const newHead = reverseList(head.next);
  head.next.next = head;
  head.next = null;
  return newHead;
};

因为代码中是使用递归实现的，需要对链表的每个节点进行反转操作，所以时间复杂度是O(n)，n是链表的长度。

代码中虽然没有产生额外的数据结构，但是这里使用递归，递归的空间复杂度主要取决于递归调用栈的空间，也就是链表的长度，所以空间复杂度是O(n)。

LeetCode算法题：题号83，删除排序链表中的重复元素

解题思路：

给定的链表是有序的
当前指针的值等于下一指针的值时，删除下一个指针。

解题步骤：

遍历链表，当前指针的值等于下一指针的值时，将当前指针的指向下下个指针。
遍历结束后，返回链表的头部。

代码实现：

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var deleteDuplicates = function(head) {
  let p = head;
  while(p && p.next) {
    if (p.val === p.next.val) {
      p.next = p.next.next;
    } else {
      p = p.next;
    }
  }
  return head;
};

因为代码中有个while循环体，循环的次数是链表的长度，所以时间复杂度是O(n)，n是链表的长度。

因为代码中没有产生额外的数据结构，所以空间复杂度是O(1)。

LeetCode算法题：题号141，环形链表

解题思路：

把这个场景想像成操场上跑步，跑的快的人，在某个时间会再遇到跑得快的人。
定义一快一慢指针，如果再某个时间两个指针能相遇，说明有环。

解题步骤：

定义一快一慢指针
如果在跑的过程在能遇到，返回true，如果快指针为null或者下一针为null，说明没有环，返回false

代码实现：

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
	let slowP = head;
  let fastP = head;
  while(fastP && fastP.next) {
    slowP = slowP.next;
    fastP = fastP.next.next;
    if (slowP === fastP) {
      return true;
    }
  }
  return false;
};

因为代码中有个while循环体，循环的次数最大的链表的长度，所以时间复杂度是O(n)，n是链表的长度。

因为代码中没有产生额外的数据结构，所以空间复杂度是O(1)。

JavaScript中的原型链

原型

原型是实例对象的共有祖先，通俗的讲，构造函数有prototype属性，由这个构造函数构造出来的实例可以访问到prototype里的属性。

function Person() {}
Person.prototype.name = "nickname"

const p = new Person();
p.name; // nickname

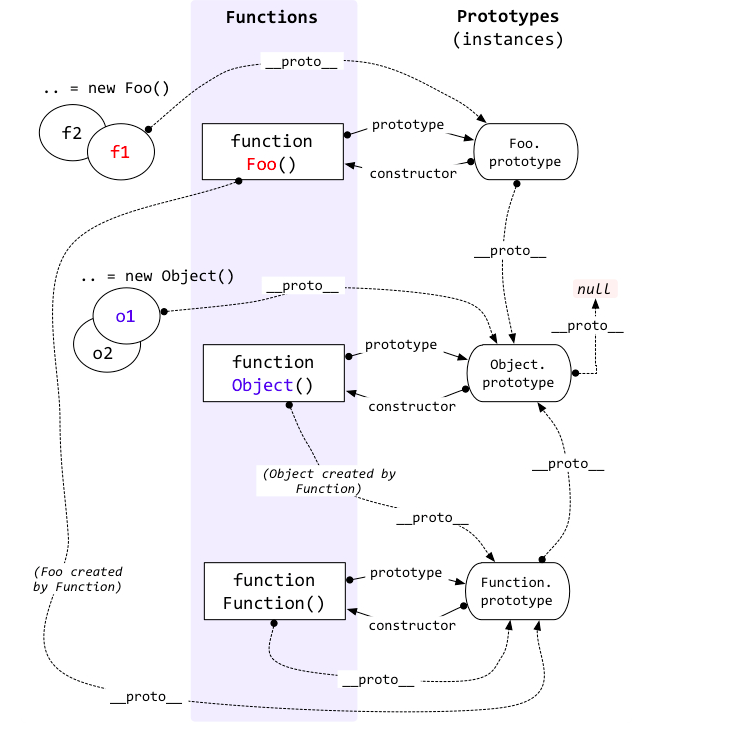
原型链

原型链本质上是链表，通过__proto__属性进行连接，每个对象都有__proto__属性，如果访问的属性不存在的时候，会沿着对象的__proto__属性去寻找，直到为null，__proto__指向构造函数的prototype对象，也就是原型。

const n = Number(1)
n.__proto__ = Number.prototype
Number.prototype.__proto__ = Object.prototype
Object.prototype.__proto__ = null

const o = Object.create({})
o.__proto__ = Object.prototype
Object.prototype.__proto__ = null

// 数组、布尔、字符串也如此
...
...
...

Instanceof的原理

记住一句话，如果A instanceof B为true，说明在A的原型链上可以找到B的原型。

实现instanceof的代码：

// 思路
// 定义一个指针
// 遍历A的原型链，如果A的原型链上有B的原型，返回true
// 遍历完之后，说明找不到，但会false
const coInstanceof = (A, B) => {
  let p = A
  while(p) {
    if (p.__proto__ === B.prototype) {
      return true
    }
    p = p.__proto__
  }
  return false
}

使用链表指针获取JSON的节点值

const json = {
  a: { b: { c: 1 } },
  d: { e: 2 },
}
const path = ["a", "b", "c"];
let p = json
path.forEach(i => {
  p = p[i]
  console.log(`${i}：${JSON.stringify(p)}`)
})

// 日志输出
// a: { b: { c: 1 } }
// b: { c: 1 }
// c: 1

最后，希望读者可以通过本篇文章对链表有一定的认识和觉悟。。。。。。

什么是链表

链表的常用操作

LeetCode算法题：题号237，删除链表中的节点

LeetCode算法题：题号206，反转链表

方法一，正向反转指针：

方法二，反向反转指针：

LeetCode算法题：题号83，删除排序链表中的重复元素

LeetCode算法题：题号141，环形链表

JavaScript中的原型链

原型

原型链

Instanceof的原理

使用链表指针获取JSON的节点值

数据结构之集合

数据结构之队列