本篇文章可以收获的知识:
-
什么是
图 -
图的常用操作 -
三道LeetCode算法题巩固
图 -
如何分析
时间复杂度和空间复杂度
什么是图
图是网络结构的抽象模型,是一组由边连接的节点,JavaScript中没有图,使用Object和Array构建图,图的表示法有领接矩阵、领接表(JavaScript中常用)、关联矩阵等,图可以表示二元关系比如:道路、航班等。
领接矩阵表示:
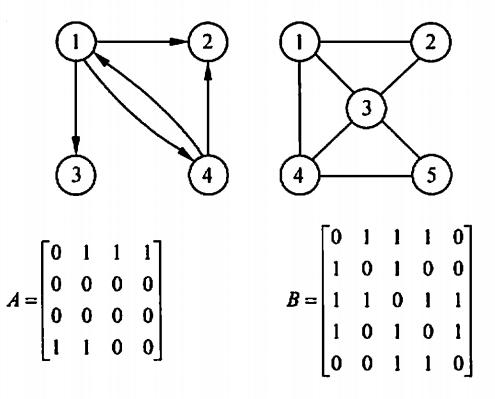
领接表表示:
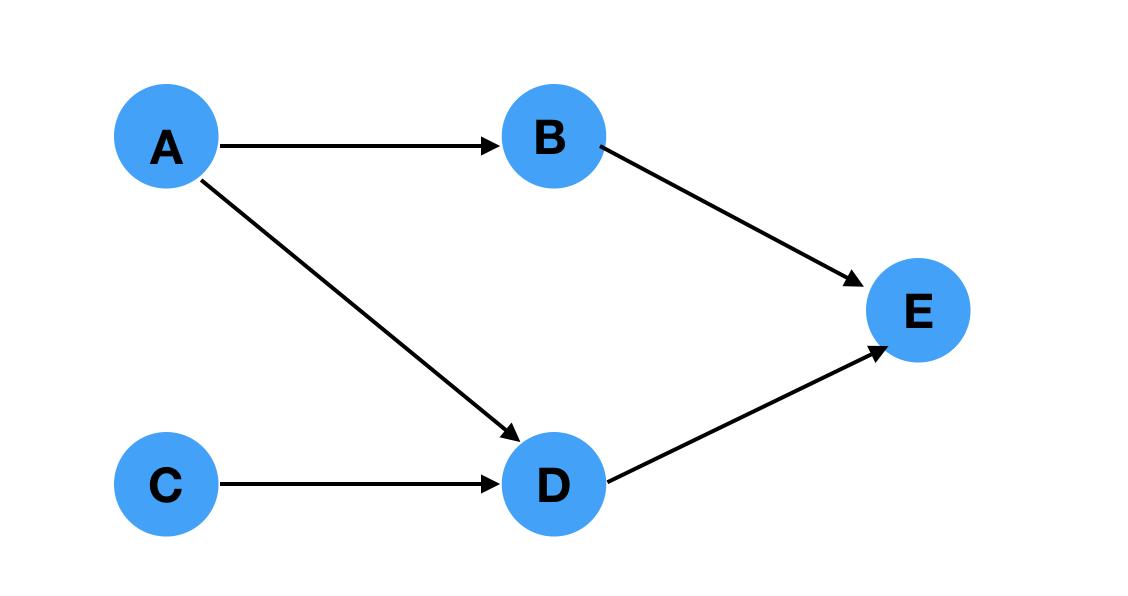
const graph = {
A: ["B", "D"],
B: ["E"],
C: ["D"],
D: ["E"],
E: []
}
图的常用操作
-
深度优先遍历
// 深度优先遍历思路 // 访问根节点 // 对根节点没访问过的相邻节点进行深度优先遍历 const graph = { A: ["B", "D"], B: ["E"], C: ["D"], D: ["E"], E: [] } const set = new Set() const dfs = (root) => { set.add(root) console.log(graph[root]) // 访问根节点 graph[root].forEach(i => { if (!set.has(i)) { dfs(i) } }) } dfs("A") -
广度优先遍历
// 广度优先遍历思路 // 新建一个队列,把根节点入队 // 把队头出队访问 // 把队头没访问过的相邻节点入队 // 重复二三步 const graph = { A: ["B", "D"], B: ["E"], C: ["D"], D: ["E"], E: [] } const bfs = (root) => { const q = [root] const set = new Set() while(q.length) { const h = q.shift() set.add(h) console.log(graph[h]) graph[h].forEach(i => { if (!set.has(i)) { q.push(i) } }) } } bfs("A")
LeetCode算法题:题号65,有效的数字
根据题目的要求,可以构建出下面的图,3、5、6是题目中所说的有效的数字
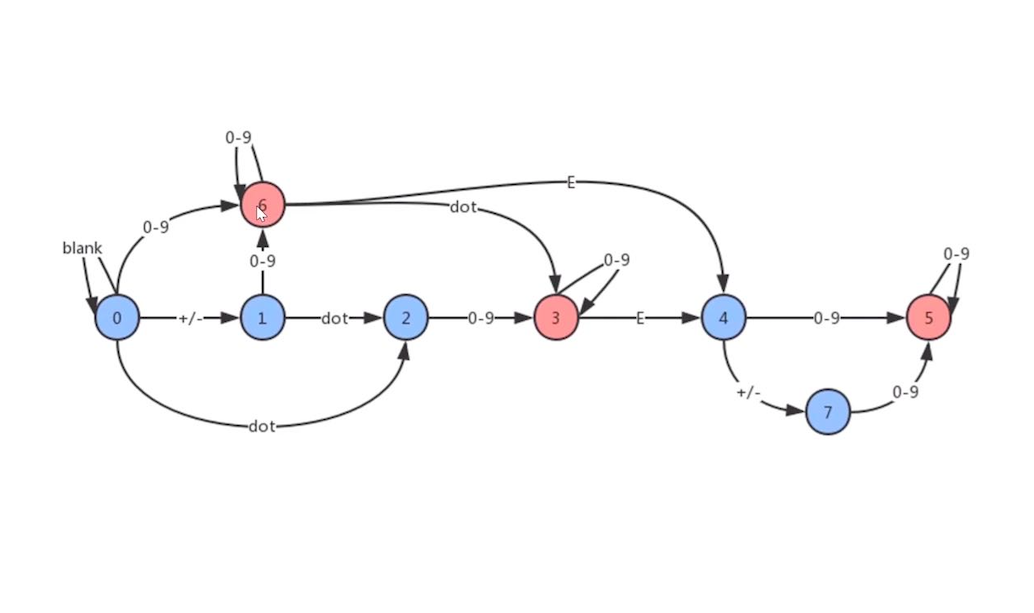
解题思路:
- 构建一个表示状态的图
- 遍历字符串,并沿着图走,如果到了某个节点无路可走,说明是个无效的数字,返回false
- 遍历结束后,如果状态在3、5、6的时候说明是有效的数字
代码实现:
/**
* @param {string} s
* @return {boolean}
*/
var isNumber = function(s) {
const graph = {
0: { "black": 0, "sign": 1, "number": 6, ".": 2 },
1: { "number": 6, ".": 2 },
2: { "number": 3 },
3: { "e": 4, "number": 3 },
4: { "number": 5, "sign": 7 },
5: { "number": 5 },
6: { "number": 6, ".": 3, "e": 4 },
7: { "number": 5 }
}
let state = 0
for (let c of s.trim()) {
if (c >= 0 && c <= 9) {
c = "number"
}
if (["+", "-"].includes(c)) {
c = "sign"
}
if (["e", "E"].includes(c)) {
c = "e"
}
state = graph[state][c]
if (state === undefined) {
return false
}
}
return [3, 5, 6].includes(state)
};
由于代码用到了for循环,循环的次数最多是字符串的长度,所以时间复杂度是O(n),n是字符串的长度。
由于代码中没有用到临时的数据结构,所以空间复杂度是O(1)。
LeetCode算法题:题号417,太平洋大西洋水流问题
解题思路:
- 把矩阵想象成图
- 从海岸线逆流而上遍历图,所到之处就是可以流到某个大洋的坐标
解题步骤:
- 新建两个矩阵,分别记录能流到两个大洋的目标
- 从海岸线,同时深度优先遍历图,过程中填充矩阵
- 遍历两个矩阵,找出能流到两个大洋的坐标
代码实现:
var pacificAtlantic = function(matrix) {
if (!matrix || matrix.length === 0) {
return []
}
const m = matrix.length
const n = matrix[0].length
const flow1 = Array.from({ length: m }, () =>
Array.from({ length: n }, () => false)
)
const flow2 = Array.from({ length: m }, () =>
Array.from({ length: n }, () => false)
)
const dfs = (x, y, flow) => {
flow[x][y] = true
;[
[x + 1, y],
[x - 1, y],
[x, y + 1],
[x, y - 1],
].forEach(([ix, iy]) => {
if (
ix >= 0 &&
iy >= 0 &&
ix <= m - 1 &&
iy <= n - 1 &&
!flow[ix][iy] &&
matrix[ix][iy] >= matrix[x][y]
) {
dfs(ix, iy, flow)
}
})
}
for (let i = 0; i < m; i++) {
dfs(i, 0, flow1)
dfs(i, n - 1, flow2)
}
for (let j = 0; j < n; j++) {
dfs(0, j, flow1)
dfs(m - 1, j, flow2)
}
const res = []
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (flow1[i][j] && flow2[i][j]) {
res.push([i, j])
}
}
}
return res
}
由于代码中遍历了整个矩阵,所以空间复杂度是O(m * n),m是矩阵的列数,n是矩阵的行数。
由于代码中使用了递归,调用的堆栈是m * n也就是堆栈的列数*行数,所以空间复杂度是O(m * n)。
LeetCode算法题:题号133,克隆图
解题思路:
- 拷贝所有的节点
解题步骤:
- 深度或者广度优先遍历所有节点
- 拷贝所有节点,存储起来
- 将拷贝的节点,按照原图的连接方法进行连接
代码实现:
/**
* // Definition for a Node.
* function Node(val, neighbors) {
* this.val = val === undefined ? 0 : val;
* this.neighbors = neighbors === undefined ? [] : neighbors;
* };
*/
/**
* @param {Node} node
* @return {Node}
*/
var cloneGraph = function(node) {
if (!node) { return }
const q = [node]
const map = new Map()
map.set(node, new Node(node.val))
while(q.length) {
const h = q.shift()
;(h.neighbors || []).forEach((i) => {
if (!map.has(i)) {
q.push(i)
map.set(i, new Node(i.val))
}
map.get(h).neighbors.push(map.get(i))
})
}
return map.get(node)
};
由于代码中使用了while循环,循环的次数是节点数,所以时间复杂度是O(n),n是节点的数量。
由于代码中使用了队列数据结构,最大的长度是节点数量,所以空间复杂度是O(n),n是节点的数量。
最后,希望读者可以通过本篇文章对图有一定的认识和觉悟。。。。。。
